Java 图的最小生成树 — prim算法和kruskal算法
一个有 n 个结点的连通图的生成树是原图的极小连通子图,且包含原图中的所有 n 个结点,并且有保持图连通的权值和边最小
一、最小生成树的应用
生成树和最小生成树有许多重要的应用。
例如:要在n个城市之间铺设光缆,主要目标是要使这 n 个城市的任意两个之间都可以通信,但铺设光缆的费用很高,且各个城市之间铺设光缆的费用不同,因此另一个目标是要使铺设光缆的总费用最低。这就需要找到带权值的最小生成树。
构建最小生成树时最常用的方法就是prim算法和kruskal算法
二、图的入度和出度
1.构建图的邻接矩阵
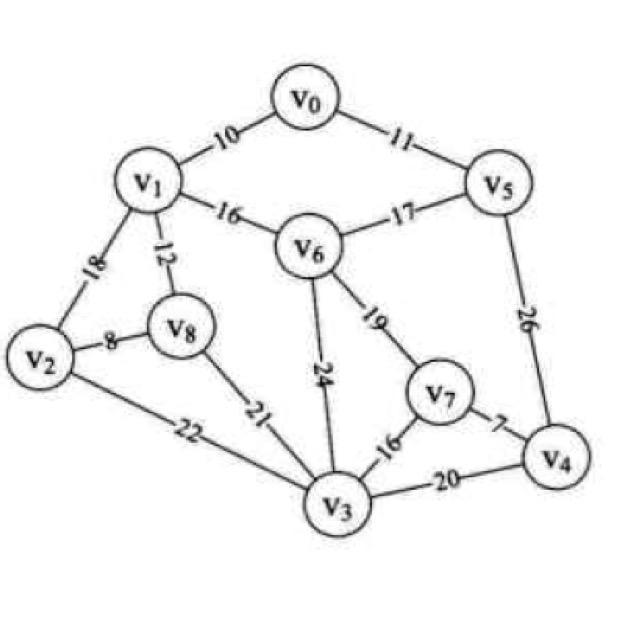
以上图中的图结构为例,由于图是顶点与顶点之间的连接关系,又带有权值,所以我们可以用邻接矩阵来表示图中顶点的关系

- 矩阵中的值代表顶点与顶点之间的权值,由于示例是一个无向图,所以这个矩阵是以对角线对称的
- 我们可以将矩阵看成一个二维数组,因此就可以很容易的创建出这个图的数据结构了
int[] graph0 = new int[]{0, 10, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 11, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT};
int[] graph1 = new int[]{10, 0, 18, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 16, MAX_WEIGHT, 12};
int[] graph2 = new int[]{MAX_WEIGHT, 18, 0, 22, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 8};
int[] graph3 = new int[]{MAX_WEIGHT, MAX_WEIGHT, 22, 0, 20, MAX_WEIGHT, MAX_WEIGHT, 16, 21};
int[] graph4 = new int[]{MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 20, 0, 26, MAX_WEIGHT, 7, MAX_WEIGHT};
int[] graph5 = new int[]{11, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 26, 0, 17, MAX_WEIGHT, MAX_WEIGHT};
int[] graph6 = new int[]{MAX_WEIGHT, 16, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 17, 0, 19, MAX_WEIGHT};
int[] graph7 = new int[]{MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 16, 7, MAX_WEIGHT, 19, 0, MAX_WEIGHT};
int[] graph8 = new int[]{MAX_WEIGHT, 12, 8, 21, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 0};
2.入度与出度
- 顶点的出边条数称为该顶点的出度
- 顶点的入边条数称为该项点的入度
- 则在矩阵中某个点的入度和出度即为横向和纵向的有效权值个数
/**
* 获取某个顶点的出度
*
* @param index 顶点序号
* @return 出度
*/
public int getOutDegree(int index) {
int degree = 0;
for (int i = 0; i < vertexSize; i++) {
int weight = matrix[index][i];
if (weight > 0 && weight < MAX_WEIGHT) {
degree++;
}
}
return degree;
}
/**
* 获取某个顶点的入度
*
* @param index 顶点序号
* @return 入度
*/
public int getInDegree(int index) {
int degree = 0;
for (int i = 0; i < vertexSize; i++) {
int weight = matrix[i][index];
if (weight > 0 && weight < MAX_WEIGHT) {
degree++;
}
}
return degree;
}
三、prim(普里姆)算法
算法思路:
- 定义一个临时的一维数组,用于存放可用的连接边,数组下标为顶点序号,值为权值
- 任选一个点作为起点,以起点的所有权值对数组进行初始化
- 找出数组中最小权值的边,即为最小生成树中的一条有效边
- 将找到的最小边在数组中赋值为0,代表已经使用过。并将数组与找到顶点的所有边进行比较,若顶点的边的权值比当前数组存放的可用边的权值小,则进行覆盖
- 重复循环2,3,4的操作直至遍历完所有顶点
算法代码:
/**
* 最小生成树,普里姆(prim)算法
*/
public void createMinSpanTreePrim() {
// 定义一维数组,存放用于比较最小权值的顶点权值,0代表已经比较过
int[] lowcost = new int[vertexSize];
// 初始化数组为第一个顶点的权值
System.arraycopy(matrix[0], 0, lowcost, 0, vertexSize);
int sum = 0;
// 循环比较
for (int i = 0; i < vertexSize; i++) {
// 先比较找出最小的权值节点
int min = -1;
for (int j = 0; j < vertexSize; j++) {
if (lowcost[j] > 0 && lowcost[j] < MAX_WEIGHT) {
if (min == -1 || lowcost[min] > lowcost[j]) {
min = j;
}
}
}
// 判断是否全部为0,找不到最小值
if (min == -1) {
break;
}
System.out.println("访问到了节点:" + min + ",权值:" + lowcost[min]);
sum += lowcost[min];
// 将当前节点的值修改成0
lowcost[min] = 0;
// 将存放最小权值的数组与下一个节点的所有连接点对比,找出最小权值
for (int j = 0; j < vertexSize; j++) {
if (matrix[min][j] < lowcost[j]) {
lowcost[j] = matrix[min][j];
}
}
}
System.out.println("最小生成树的权值总和:" + sum);
}
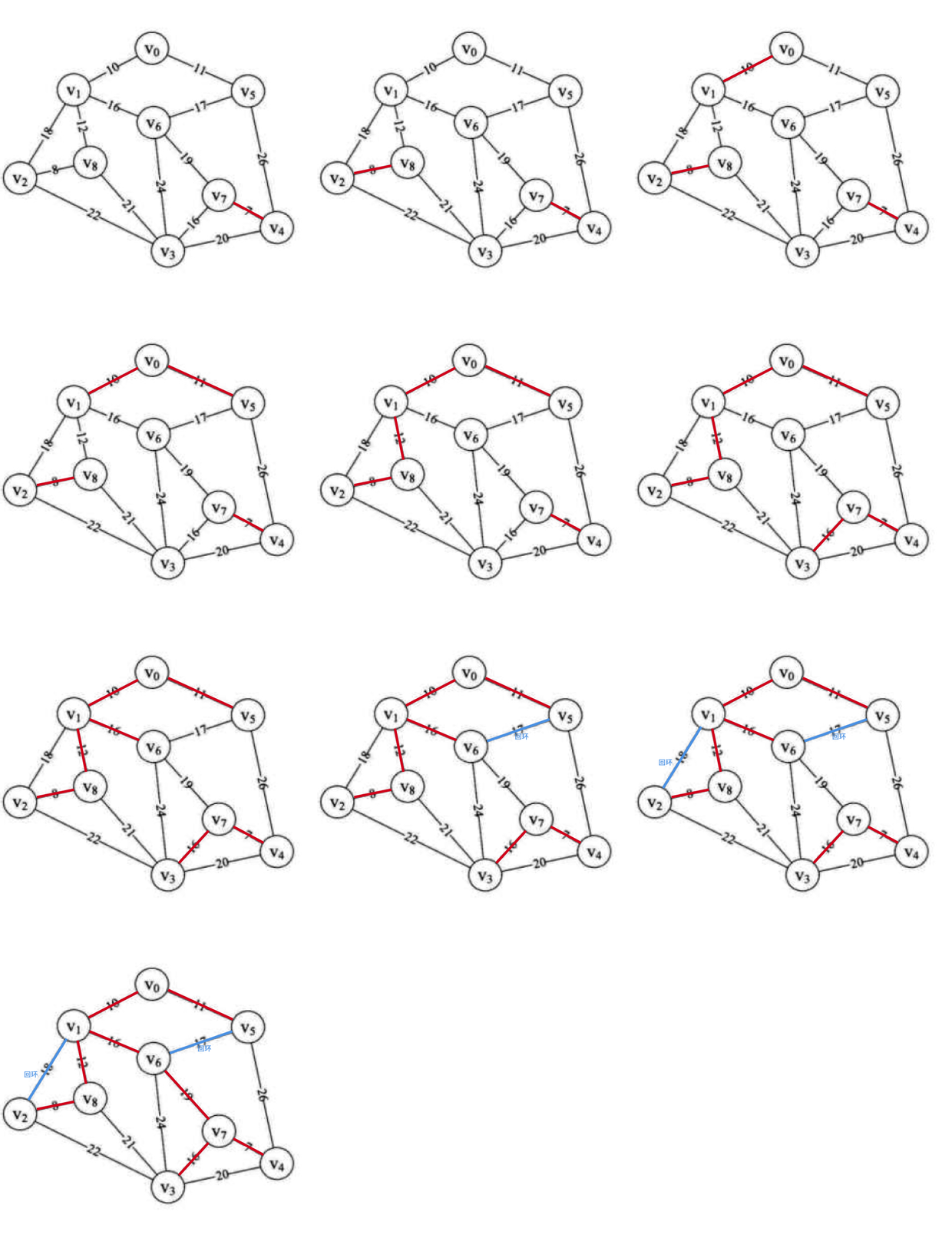
下图是画的一个针对此代码运行的流程图(画了半天发现在文章中显示的比较小,如果看起来觉得小的同学可以下载原图后放大观看)
- 绿色代表一维数组中存放的可用最小边
- 红色代表找到的最小生成树的边
四、kruskal(克鲁斯卡尔)算法
算法思路:
- 现将所有边进行权值的从小到大排序
- 定义一个一维数组代表连接过的边,数组的下标为边的起点,值为边的终点
- 按照排好序的集合用边对顶点进行依次连接,连接的边则存放到一维数组中
- 用一维数组判断是否对已经连接的边能构成回路,有回路则无效,没回路则是一条有效边
- 重复3,4直至遍历完所有的边为止,即找到最小生成树
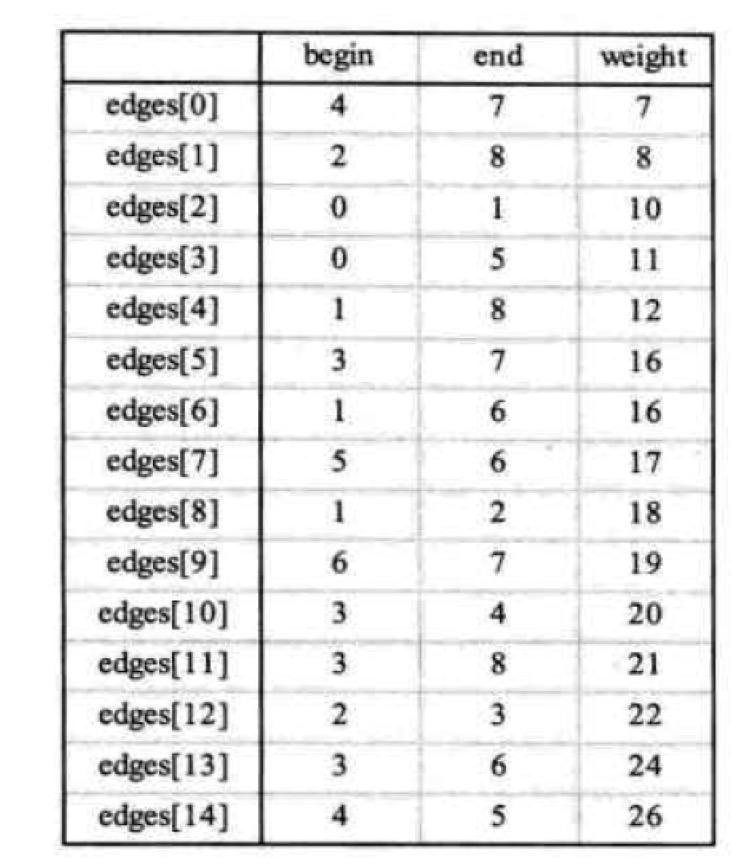
首先将所有边按权值进行排序
定义一个边的对象
/**
* 连接顶点的边
*/
class Edge {
private int start;
private int end;
private int weight;
public Edge(int start, int end, int weight) {
this.start = start;
this.end = end;
this.weight = weight;
}
}
按照排序的图对边进行初始化
Edge edge0 = new Edge(4, 7, 7);
Edge edge1 = new Edge(2, 8, 8);
Edge edge2 = new Edge(0, 1, 10);
Edge edge3 = new Edge(0, 5, 11);
Edge edge4 = new Edge(1, 8, 12);
Edge edge5 = new Edge(3, 7, 16);
Edge edge6 = new Edge(1, 6, 16);
Edge edge7 = new Edge(5, 6, 17);
Edge edge8 = new Edge(1, 2, 18);
Edge edge9 = new Edge(6, 7, 19);
Edge edge10 = new Edge(3, 4, 20);
Edge edge11 = new Edge(3, 8, 21);
Edge edge12 = new Edge(2, 3, 22);
Edge edge13 = new Edge(3, 6, 24);
Edge edge14 = new Edge(4, 5, 26);
最小生成树算法代码:
/**
* kruskal算法创建最小生成树
*/
public void createMinSpanTreeKruskal() {
// 定义一个一维数组,下标为连线的起点,值为连线的终点
int[] parent = new int[edgeSize];
for (int i = 0; i < edgeSize; i++) {
parent[i] = 0;
}
int sum = 0;
for (Edge edge : edges) {
// 找到起点和终点在临时连线数组中的最后连接点
int start = find(parent, edge.start);
int end = find(parent, edge.end);
// 通过起点和终点找到的最后连接点是否为同一个点,是则产生回环
if (start != end) {
// 没有产生回环则将临时数组中,起点为下标,终点为值
parent[start] = end;
System.out.println("访问到了节点:{" + start + "," + end + "},权值:" + edge.weight);
sum += edge.weight;
}
}
System.out.println("最小生成树的权值总和:" + sum);
}
/**
* 获取集合的最后节点
*/
private int find(int parent[], int index) {
while (parent[index] > 0) {
index = parent[index];
}
return index;
}
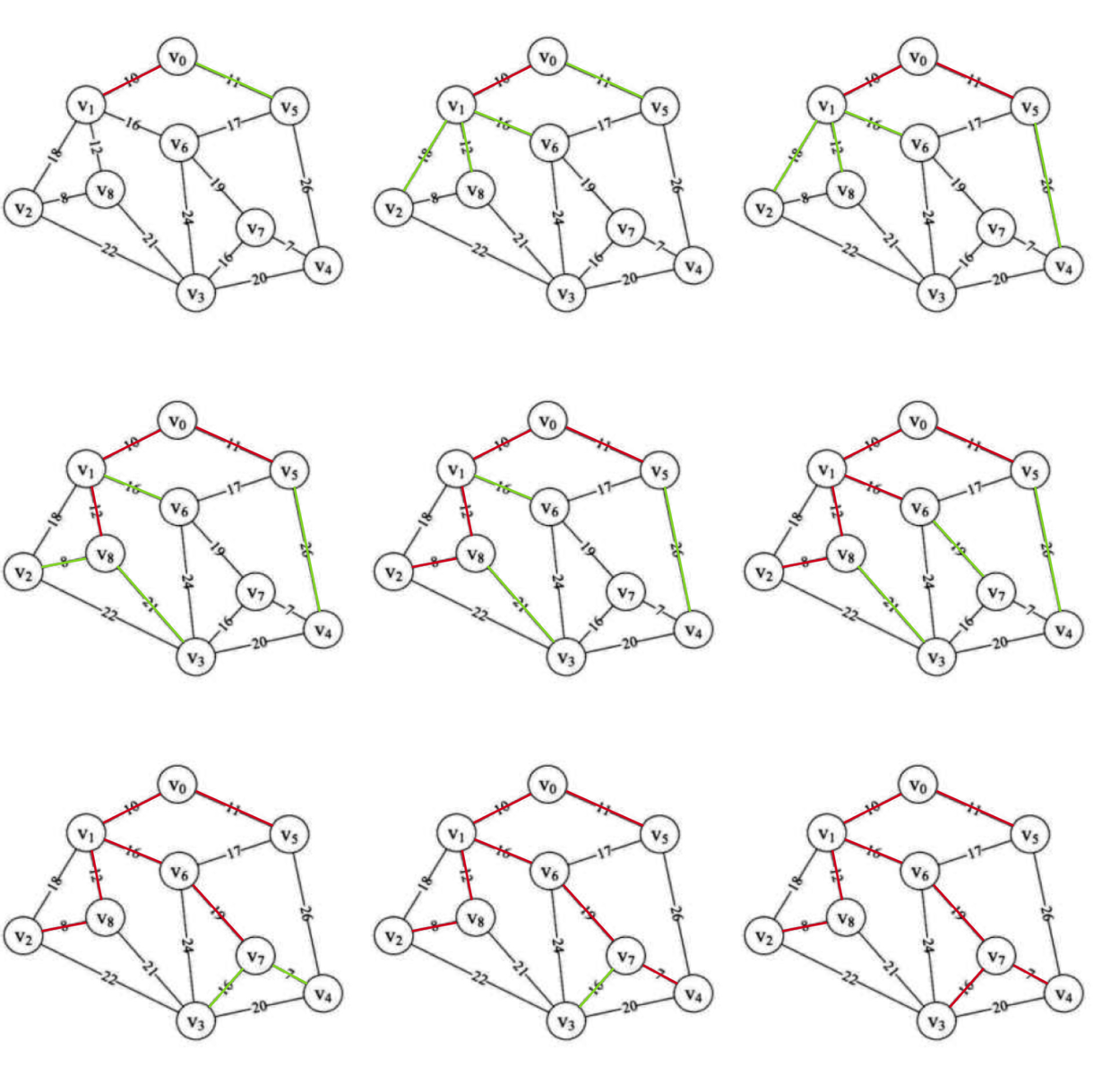
下图是画的一个针对此代码运行的流程图
- 红色代表找到的最小生成树的边
- 蓝色代表找到的边但是是回环则无效